声屏障降噪理论及计算方法

      道路声屏障降噪理论研究从发展历程和基本特点来看可以分为三种，即几何与波动声学理论、试验与半经验理论以及边界元理论。

1.波动与几何声学理论

  声屏障波动与几何声学理论可以归结为研究声波的衍射问题。其最初来源于光学，通过求解具有一定边界条件的波动方程，得到衍射声场中各受声点的声压。但几何和波动声学理论对于声屏障表面为有限阻抗或部分有限阻抗的情况未给出明确的理论解，与实际应用中声屏障表面是有限阻抗或变化阻抗的情况有一定差距。另外按照声屏障的实际尺寸，该理论更适用于中高频噪声，但根据我国道路交通状况，实际交通噪声的等效频率较低。在大型车出例较高或车速较慢的城市道路上，等效频率甚至更低，因而该理论与实际道路交通噪声有一定差距。目前一些声学模拟软件是建立在几何与波动声学理论上的，如声学软件Raymone。

2.试验和半经验法

试验和半经验法是目前我国计算声屏障降噪效果采用的主要方法。试验和半经验法是结合几何声学理论和实验结果所得到的经验性公式，它仅仅预测声场中的声强度分布。它以单一的无量纲菲涅尔数N为参量来计算重直刚性声屏障的插入损失，是美国和英国目前交通噪声预测的基础。我国在进行声屏障插入损失的预测时也多采用此法。

菲涅尔数N定义为

                                δ         fδ

                     N= 2^_____ =2^_____

                                 λ         c

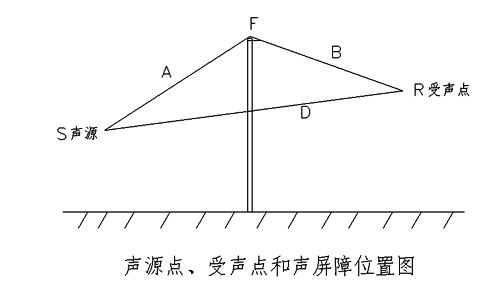
式中  δ一声程差，6=A+B-D，见图21；

         λ一点源发声的波长；

         f 一入射声波的频率；

         c 一声速。

       试验和半经验理论山于采用单一无量纲菲涅尔数，使计算非常简单，为我国目前进行声屏障设计时的主要计算方法。但该方法只能对刚性垂直薄屏障进行插入损失计算，对于声屏障表面为吸声型或部分吸声型以及复杂结构声屏障尚不能求解。另外试验和半经验理论计算声屏障插入损失时并没有考虑声屏障透射声能的影响，因此声屏障隔声量必须足够大，大于目标插入损失10d日以上、才不至于影响声屏障的插入损失计算精度。

3.边界元法

     边界元方法是将描述弹性力学偏微分方程的边界值问题化为边界积分方程并吸收有限元法的离散化技术而发展起来的。目前广泛应用的边界元理论来源于Helmholz积分方程。

     边界元法是一种数值方法，为中低额声的无界声场的求解提供了可能。从理论上利用边界元方法进行数字模拟分析不受实地条件的影响，主要依赖于计算机的计算，故能快速得出计算结果，利用边界元法来模拟分析不同形状和声学特性的声屏障的降噪效果可以有效而快速地为今后高效产屏障的设计提供方向和参考依据。应用边界元理论求解声屏障的插入损失，可以很方便地考虑产屏障的不同几何形状、声源的指向性及地面和声屏障的表面吸声条件。

由了边界元法的优点，得到研究者的广泛重视。一般求解声屏障插入损失理论是假定在二维情况下进行的，近年来结合计算机技术的应用、边界元理论的研究已经发展了一些模型，可以考虑气象条件的影响，如风、温度阶梯、气流和大气折射等。但对于高频，边界元数目很大，计算量也很大。因面边界元理论更适合于中低额声屏障插入损失的计算。日前边界元法还处在理论探讨阶段，在声屏障领域的实际应用还是比较少的，该种方法同样也避免不了声副定义的问题，这是目前声屏障降噪效果计算的关键。